探索单个频段调制中的织布工调制器的实践原理

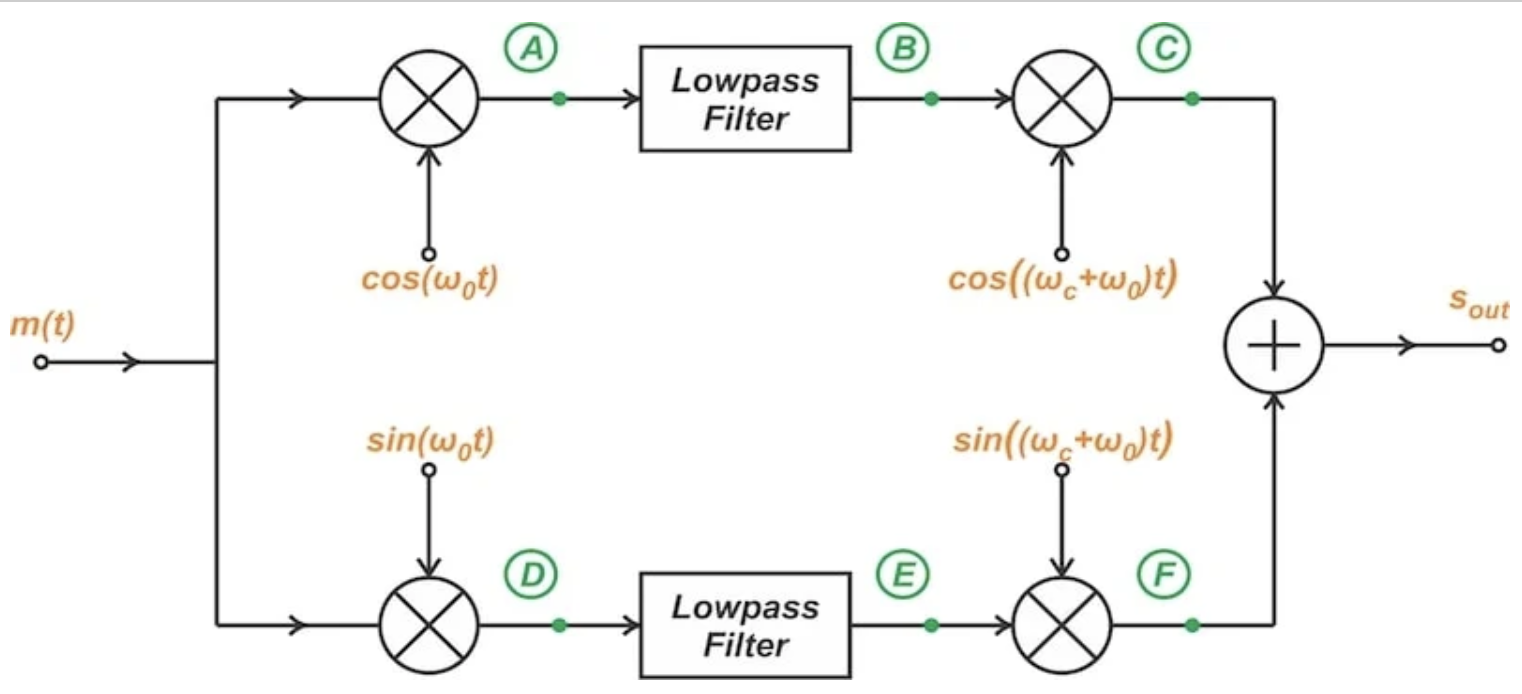我们逐步介绍了织布机调制器如何使用图形表示来允许数学分析来转换信号的频谱。本文引用：与传统的振幅调制（AM）相比，单个侧面调制（SSB）节省了很多带宽和功率。该系列解释了生成SSB信号的三种方法。这些方法如下所示，按实现顺序：过滤方法。相位方法。 Weaver方法上一篇文章讨论了由单个频率消息信号的基本原理使用的编织方法。正如我们了解到的那样，织布机调制器不需要用于过滤方法的锋利带阶滤波器。它也是上面提到的三个选项中最实用的，因为它不需要相位方法中的精确的相变杠杆。图1显示了编织器调制器电路图。在本文中，我们将通过检查如何修饰输入频谱来继续研究电路d通过上图中标记的六个节点（a f。nodes a c a c a c a up）。在下部信号途径上发现节点D A C。接下来，我们检查通过将上和下通光谱组合来创建的输出光谱。图2显示了一个带有B的带宽的输入频谱，首先，让我们看一下将上游路线与Coseno Wave混合的上游路线。使用Euler方程，术语余弦可以表示如下：在Weaver方法中，第一对乘数将消息信号与振荡器混合在一起，并在消息信号的频率范围的中心中将消息信号混合在一起。 Banda B占用的消息信号，因此有F 0 = B/2。因此，第一个乘数会产生两个信号。频谱上升f 0，其他低光谱相同。在这两种情况下，信号的幅度都降低到一半。图3（b）显示了乘数输出频谱（方案中的节点A）。为了使分析更容易理解赖光谱成分和向下以颜色区分。绿色看着，蓝色升起。图3垂直轴的两半都是{。 }这些光谱成分对应于信号光谱的实际部分。与织布工调制器下方使用的混合器不同，输入到和节点A之间的混合过程不会将入口信号的实际部分转换为虚构部分。从节点A，信号传递到低通滤波器到B/2切割频率。图4显示了滤波器输出的光谱（节点B）。低通滤波器输出信号将输入第二个乘数，并与余质波混合，频率为f c+f 0 = f c+b/2。与第一个乘数相似，上层路线上的第二个乘数将光谱转换为±（F C+ B/2），并将振幅乘以额外的系数为0.5，与输入光谱相比，一般尺度系数为0.25。图5（d）显示了第二个乘数（节点C）的出口光谱。通常，图5显示了入口路由的信号光谱如何通过。在大多数方面，下部路由功能与上路线的功能相似。区别在于，入口与正弦波混合，并引入90度的相变。使用Euler的方程式，正弦波函数可以写如下：上升变化的频谱乘以因子1/（2）= –0.5，而下降的变化分量则接收到尺度因子–1/（2）= 0.5。单位的存在意味着输入频谱的实际部分在第一个乘数（节点d）的输出处变为虚构数字。结果是图6（b）所示的频谱。垂直轴为{。 } im {接下来，一个b/2切割频率的低通滤波器除了通过频带以外的所有频率组件。图7显示了滤波器输出的频谱。最后，较低路线上的第二个乘数会改变频谱±（f c+ f 0）=±（f c+ b/2）。为了繁殖正弦波函数，上升的组成部分的幅度分别变化，分别降至-0.5和+0.5倍。但是，应用于第二个乘数（图7）的光谱在垂直轴旁边是IM。 }对于符号，它已经具有隐式比例因子。因此，上升变化和下降变化的组成部分分别攀升为-0.5×= 0.5和+0.5×= –0.5×。这意味着假想部分返回到实际部分，如图8所示。垂直轴是IM {。 } re {。请注意，它已更改为}。图9显示了下面路线上所有节点的频谱。通过组合C和F节点的光谱分别表示上下路线来获取输出光谱。这些光谱如图5（d）和9（d）所示。但是，为了更轻松地可视化，图10可以追溯到两个SPECTRUM和最终输出频谱。您可以看到上部带显示在出口处。下条带已消除。图11总结了编织器调制器的分析。它显示了所有节点的信号频谱，包括电路输入和输出。一些作者选择了一种略有不同的方法来表示与低路线相关的光谱成分。在图12中，在垂直轴旁边，我们使用此方法在下部路线上显示节点d，e和f的光谱。要完成，让我们使用此表达式来轻松验证您的分析。由于入口M（t）与正弦波混合，因此图12（b）中升高变化的光谱成分的比例因子为1/2。图12（b）中下降变化的光谱成分的比例因子为-1/2。低通滤波器消除了先前的组件B/2而不会改变比例系数，从而导致图12（c）的频谱。最后，第二个混合器e下路由将向上的组件乘以1/2，将组件乘以-1/2。图12（c）中的绿色组件已经具有比例因子-1/2，因此图12（d）的副本和下降具有总比例因子（-1/2）×（1/2）= 1/4 = 1/4和（-1/1/2）×（-1/1/2）= -1/4。同样，图12（c）中的蓝色组件已经具有1/2的比例因子。因此，该组件的上部和下部副本具有（1/2）x（1/2）= –1/4 y（1/2）x（1/2）x（–1/2）= 1/4。将图12（d）与图11进行比较，该结果与先前的分析一致。你知道。本系列的先前文章讨论了唯一的频率消息信号的概念，并讨论了应用复杂的基本频段表示的Weaver方法的基础。在本文中，我们将使用任何频谱来更详细地探索调制器操作。我希望将这些讨论结合在一起，以帮助构建此有用的SSB电路效果很好。本文也是如此在RF系统中，介绍了一系列15个部分的最后一部分。以下是所有EST ARTICLESTO系列的完整列表。